Tests on hardened concrete: Schmidt or Rebound hammer test and core drill test

thaerZagel 4 Comments

Several tests can be carried out on hardened concrete to check its quality. These tests are divided into two groups namely: nondestructive tests on hardened concrete and destructive lab tests on hardened concrete. As their names suggest, non destructive tests check the quality of concrete without destroying the sample, and are useful in examining concrete at work sites. Destructive tests on the other hand are lab tests that check the quality of hardened concrete by finding the maximum stress the samples can handle before failure. Crushing of cubic and cylindrical concrete samples is the most common destructive test.

Core test on hardened concrete column

In the previous lab, two tests on hardened concrete were carried out. The first is the Schmidt hammer test which is a nondestructive test that aims to measure the surface hardness of a mass of concrete by impacting the concrete surface with a specified mass activated by a standard amount of energy, finding the rebound number, and then using it in calculating the surface hardness. This test is not highly accurate and only gives an indication about surface hardness.

The second test that was carried out is the core test. This test is used as one of the last resorts in checking concrete quality when crushing cubic or cylindrical samples at 28 days indicates failure of concrete or when suspicious concrete used in structural elements (such as beams, slabs, and columns) fail in nondestructive tests such as ultrasound test and Schmidt hammer test. The test is highly accurate and is even used as evidence in court rooms. In the lab, a sample will be taken from a beam.

 

Aim and objectives

The aim of the Schmidt hammer test is to get an indication about the average surface strength of different concrete samples, a concrete beam, and a piece of building stone.

The aim for the core test is to measure the compressive strength of a core sample taken from a beam by drilling.

 

Theory and prediction:

For Schmidt hammer test:
➦ The Schmidt hammer measures the rebound of a spring loaded mass impacting against the surface of the sample. The test hammer will hit the concrete at a defined energy. Its rebound is dependent on the hardness of the concrete.

➦ By reference to the conversion chart, the rebound value can be used to determine the equivalent cube compressive strength. The higher the rebound number, the higher this strength value.

➦ When conducting the test, the hammer should be held at right angles (90, 0, or -90 degrees) to the surface which in turn should be flat and smooth. The rebound reading will be affected by the orientation of the hammer when used in a vertical position. On the underside of a suspended slab for example (ф= 90°), gravity will increase the rebound distance of the mass and vice versa for a test conducted on a floor slab (ф= -90°).

➦ The test is sensitive to local variations in the sample. To minimize this it is recommended to take a selection of readings and take an average value.

➦ It is also recommended to eliminate any values differing from the average by more than 15 % since the error values for the Schmidt hammer range from 13-32%


For the core test:
➦ Concrete core drilling is the process of drilling perfectly round holes through concrete walls, floors and other concrete structures to obtain test samples. Core drill test is the second most reliable test for determining concrete strength after the crushing test.

➦ A concrete core drill bit consists of a steel tube with diamond segments brazed or laser welded on the drilling end. The core bits are mounted on the rotating shaft. A supply of water is needed for lubrication and to prevent the over-heating of the drill.

➦ A standard core sample has a length/diameter ratio of 2/1. If the sample’s ratio is higher, strength is multiplied by a factor lower than one. the strength of higher ratios on the other hand is multiplied by a factor greater than one. The values of these factors are obtained from tables.

The strength of a standard cylinder is obtained by the following equation:
Strength (standard cylinder) = strength (test cylinder) * (l/d)factor

The strength of a standard cube is obtained by the following equation:
Strength (standard cube) = strength (standard cylinder) * 1.25

➦ The test sample cylinder is capped with sulfur at both ends to even out the surface so that the load is distributed equally along the loaded surfaces.

➦ The cores to be tested must saturated with water. Therefore, they must be kept in water for at least 72 hours.

 

Tools and instruments:

The following tools were used For Schmidt hammer test:
  1. A Schmidt hammer.
  2. Five small cubes of hardened concrete (10*10*10 cm).
  3. One large cube of hardened concrete (15*15*15 cm).
  4. Two small cylinders of hardened concrete 15 cm height and 15cm diameter.
  5. Beam of hardened concrete, 150 cm long and having a 15x10 cm cross section.
  6. A rectangular piece of building stone.

The following tools were used for the core test:
  1. Core drilling apparatus.
  2. Beam of hardened reinforced concrete.
  3. Crushing apparatus.
  4. Sulfur coating.
  5. Caliper measuring device
  6. Weighing balance.

Procedure:

For Schmidt hammer test:
  1. Several points were marked with chalk on one of the faces of a 10*10*10 concrete cube.
  2. The Schmidt hammer was inserted above one of the points with its top facing downwards (ф= -90°) and was compressed by manually until it rebounded.
  3. The button on the hammer was pressed to hold the pointer in place and fix the reading, and the reading on the scale was recorded.
  4. The last two steps were repeated for the other points on the cube.
  5. The procedure mentioned above was repeated for the other small cubes, the large cube, and the two cylinders. For each sample, 3-5 values of the rebound number were taken at different places along the surface.
  6. The same procedure was repeated for a beam of hardened reinforced concrete. This time however, the Schmidt hammer was carried horizontally (ф= 0.0°). 14 readings were taken.
  7. For the stone the same procedure was repeated for two hammer positions: horizontally (ф= 0.0°), and pointing downwards (ф= -90°). For each position two readings were taken.
  8. The average of readings for each sample was calculated. Any values differing from it by 15% were excluded and the new corrected average was calculated. Based on this average, the average strength was found from graphs.


For the core test:
  1. The beam was inserted below the drill so that the region in which the cut will be made was directly under the drill’s cutting cylinder.
  2. The drill was turned on and the water valve was opened so that water cooled and lubricated the cutter as it cut through the sample.
  3. One the steel bars were reached, cutting was stopped and the sample was obtained.
  4. The sample was submerged in water for 7 days.
  5. The sample weight in air (saturated surface dry), and its submerged weight were measured.
  6. The sample was inspected after seven days for the maximum aggregate size and the maximum size of aggregates.
  7. The sample dimensions were measured with a caliper and the sample faces were rammed before coating them with sulfur.
  8. The sample was crushed and its strength was recorded.


Data and calculations:

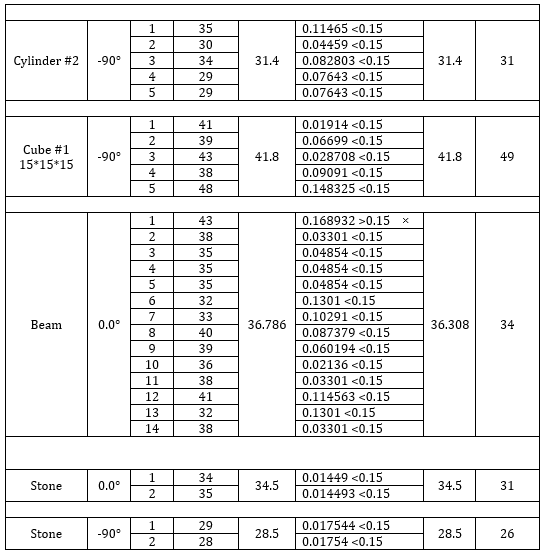
For Schmidt hammer test:
The following table summarizes the data obtained for this experiment as well as the calculations performed:




Sample calculations (for the beam):





Upper bound for accepted readings = avg. +15% = 1.15 * 36.786 = 42.30
➠The first reading (43) is excluded
Lower bound for accepted readings = avg. -15% = 0.85 * 36.786 = 31.27
➠ New Avg. = (515-43)/13 = 36.308
➠ From tables, based on this average rebound number, the strength for angle Ф=0.0° is 34 MPa.



For the core test:
The following table summarizes the data obtained for this experiment as well as the calculations performed:

Table (2): data and calculations for the core test
Date of casting
35 days before performing the test
Date at test
9-November-2009
Age at test (days)
35 days
Location of casting
A test reinforced beam in the lab
Weight in air
1357 grams
Weight in water
790 grams
Volume: for rammed sample
               for unrammed sample
444869.87 mm3 = 444.87 cm3
567000 mm3 = 567 cm3
Density
2.39 g /cm3
Length of specimen before cap
104.85 mm
Length of specimen after cap
112.75 mm
Thickness of sulfur
7.9 mm
Diameter of specimen (mm)
73.5
Max size of voids
3.80 mm
Max size of aggregates
24.1 mm
Cross-sectional area of specimen
4242.92 mm2
Length/diameter
1.427
Strength (kN force)
83.4 kN
Standard cylinder strength
18.87 MPa
Cube strength
23.6 MPa


Calculations:
Volume (unrammed sample) = Wssd-Wsub = 1357-790 = 567 cm³
Volume (rammed sample) =π r² L= π (7.35/2)² *10.485 =444.87 cm³
The density of concrete = (Wssd / (Wssd-Wsub)) = (1357 / (1357-790)) = 2.39 g/cm³
The thickness of sulfur = 112.75-104.85 = 7.9 mm
Cross sectional area = π r² = 3.14*(73.5/2)² = 4242.92 mm²
Length/diameter = 104.85 / 73.5 = 1.427 < 2
Lab cylinder strength = F/A = (83.4*1000)/4242.9 = 19.66 MPa
Standard cylinder strength = Lab cylinder strength * (L/D factor) 
                                           = 19.66 * 0.96 = 18.87 MPa
Cube strength = 1.25* cylinder strength = 1.25*18.87 = 23.59 MPa

 

Results and Conclusion:

The results of the experiment can be summarized as follows:

Result and conclusion For Schmidt hammer test:
The main results for this experiment are the strength values for concrete samples, the beam, and the stone samples. For these results, please refer to the data and calculations section (table 1).

It is known that the Schmidt hammer test is inaccurate and that the error in readings can reach 13-32%. For this reason, the test is used as an indication about the quality of hardened concrete and is not considered a standard reliable test. To minimize the error, several reading were taken for every sample and any reading deviating from the mean by more than 15% was excluded and the strength value was estimated based on the new average after excluding improper results. This was done to give a better indication about the surface hardness of the samples.

Since nothing is known about the age of the concrete samples or their intended strength, comparison between their strength values would be meaningless. Generally speaking however, the cylinders gave the lowest strength and the large cube gave the highest strength. Strength values of the small cubes ranged from 31 (cube 3) -38.5 (cube 1). The rebound numbers for cylinders were lower than the small cubes because they are longer which means that their stability is lowest as the mass collide and rebound on them. The large cube had the highest rebound numbers because it has the largest cross sectional area so it is the most stable. Large cubes are expected to give the most accurate results and the least distortion.

It is also important to bear in mind that the value of rebound number (and thus the value of strength) is affected by the surface conditions of the sample being tested. The presence of aggregate on the surface will give a higher rebound number and thus a higher strength because aggregates are usually stronger than the mortar in between and have harder surfaces. On the other hand, if a crack or an air void is present in the place were the hammer is rebounded or nearby it, the rebound number (and thus the strength) will be highly reduced because rebound increases as surface strength increase. These two reasons explain why the values of rebound numbers varied from place to another on the same surface along the beam. The same thing also applies to the other samples. For these reasons, the chosen points should be inspected so that no visible cracks or aggregate are present to obtain reliable results.

Additionally it is important to mention the angle of rebound because a -90 angle will give the highest strength at a given rebound number (because the mass in hammer is accelerated and pulled down by gravity), angle 0.0 will give intermediate rebound and angle 90 will give the lowest strength for a given rebound number. For the stone the rebound values and strength were higher for Ф=0° than for Ф=-90°. The reason for this is that at the first angle, the hammer was rebounded at the smaller surface area and rebounds were resisted by the larger one which gave higher readings. The opposite occurred for Ф=-90°.

Possible sources of error in this experiment include:
§ Systematic errors and inaccuracy of the hammer apparatus used.
§ Errors in angles setting (angles were not exactly -90 or 0.0 degrees).
§ Inaccuracy of strength values since they were approximated from graphs.
§ Surface hardness was measured and not the actual strength of the concrete mass.
§ The test is sensitive to the water content of the sample; a saturated material will give different results from a dry one.


Result and conclusion for the core test:
The results for this experiment can be summarized as follows:

Standard cylinder strength =18.87 MPa
Cube strength = 23.59 MPa

The core drill is a very reliable test for determining the strength of hardened concrete being used in structural form and is used as a last resort for testing whether the concrete strength is accepted before destroying it. The standard cylinder has a ratio of length: diameter equals 2:1, the lower this ratio for the taken sample, the higher the strength, and thus the strength of lower ratios is multiplied by a factor lower than one and the strength of higher ratios is multiplied by a factor higher than one determined from tables. The reason for this is that higher L/D ratios make samples less stable and increases the possibility of buckling.

The diameter of the cylinder should be at least 3 times the maximum aggregate size and this is true for this experiment where 73.5 >3*24.1. The larger the sample, the more accurate the results would be. To obtain accurate results, the strength value should be multiplied by an age factor and sample size factor in addition to the L\d factor. Since this is not done in this experiment the results are not highly accurate but could be easily modified to obtain an accurate strength value.

Engineering use:

The Schmitt hammer test has the following engineering uses:
➦ To give an indication about concrete surface hardness and thus its strength as well as an indication about the rate of increase of strength with time.

➦ To determine whether or not a core test should be drilled based on the approximate strength given by the Schmitt hammer test.

➦ To determine were exactly to take core test samples based on the strength values given by the Schmitt hammer test.

➦ To approximate the amount of damage done to structures due to external factors such as fire or earthquakes.

➦ To approximate concrete strength in old structures.


The core drill test is used to test the strength of concrete that is being used in structures if there is high evidence that the concrete didn’t achieve the desired strength. The evidence could be the results of cube and cylinders crushing at 28 days as well as the indications of nondestructive tests such as hammer test and ultrasonic test. The test is also used to test the concrete of old building when a high loss of strength is suspected and nondestructive tests indicate this.
Tags :

Related Posts

Post a Comment

4 Comments

  1. marksonApril 13, 2021 at 4:31 AM

    Besides, the report likewise gives a reasonable image of the condition of both customary and developing business sectors. Makita drills

    ReplyDelete
  2. justinJune 27, 2021 at 7:08 AM

    Concrete crusher machines are growing in popularity as business seek a way to reduce the cost and environmental impact of recycling concrete at demolition sites. Learn more about concrete crushers, and the types of machines available. Click Here

    ReplyDelete
  3. newprofileJune 27, 2021 at 8:25 AM

    Concrete crusher machines are growing in popularity as business seek a way to reduce the cost and environmental impact of recycling concrete at demolition sites. Learn more about concrete crushers, and the types of machines available. Click Here

    ReplyDelete
  4. MichealSeptember 18, 2024 at 1:24 AM

    "Work was done quickly and professionally." concrete installers

    ReplyDelete