Flow Measuring Apparatus - Fluid Mechanics Laboratory
Abstract
This article represents a method for measuring the mass flow rate through three different methods which are the venturi-meter, the orifice, and the rotameter. This actual mass flow rate is then compared to the theoretical mass flow rate found using specific equations. The discharge coefficient for the three methods will also be calculated and compared to acceptable values.
The rotameter consists of a transparent tapered tube in which a float takes up an equilibrium position of this float assessed from the scale on the wall of the rotameter, is a measure of the flow rate. Manometer tubes for measuring pressures are connected to points A, B, C, D, E, F.G, H and I.
We first switch on the hydraulic bench, then adjust the bench supply valve on the hydraulic bench, then press on the manifold outlet to lower all manometer readings, after that we adjust the bench supply valve to raise the rotameter to specific high, record hA, hB, hE and hF. After that measure the mass flow rate, at the end convert all the rotameter readings (cm) to (m Kg/s).
Objectives
- To measure and calculate the actual and theoretical mass rates for the venturi-meter, and the Orifice.
- To calculate the discharge coefficient of the venturi-meter, the orifice, and the rotameter.
- Calibrate the rotameter to give the actual discharge directly.
Data and calculation
Weight = 12 KgTable 1 - The collected data
| - | Venturi | Orifice | - | ||||
|---|---|---|---|---|---|---|---|
| Run | hA (mm) | hB (mm) | hE (mm) | hF (mm) | Time (sec) | Rotameter (cm) | Rotameter (Kg/s) |
| 1 | 355 | 135 | 327 | 244 | 25.69 | 20 | 0.43 |
| 2 | 315 | 135 | 305 | 117 | 27.15 | 18 | 0.39 |
| 3 | 283 | 140 | 274 | 125 | 32.25 | 16 | 0.35 |
| 4 | 255 | 140 | 264 | 127 | 37.5 | 14 | 0.31 |
| 5 | 227 | 144 | 222 | 135 | 41.78 | 12 | 0.27 |
| 6 | 205 | 142 | 200 | 134 | 49.94 | 10 | 0.24 |
| 7 | 187 | 142 | 184 | 137 | 60 | 8 | 0.19 |
| 8 | 172 | 144 | 169 | 139 | 77.22 | 6 | 0.15 |
Calculations
1. To find the actual mass flow rate (ṁact):

ṁ ≡ Mass flow rate [kg/s]
t ≡ Time [s]
m ≡ Mass of weights = 12 [kg]
2. To find the mass flow rate using the Venturi-meter (ṁvnt):


3. To find the mass flow rate using the Orifice-meter (ṁorf):


4. To find the coefficient of discharge for the venture meter (Kvnt):
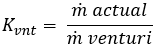
5. To find the coefficient of discharge for the orifice meter (Korf):

6. To find the coefficient of discharge for the Rotameter (Krota):

Sample calculation for run No. 1:
1. To find the actual mass flow rate (ṁact):

2. To find the mass flow rate using the Venturi-meter (ṁvnt):

3. To find the mass flow rate using the Orifice-meter (ṁorf):
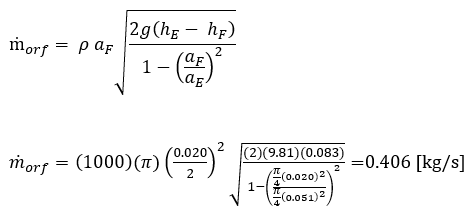
4. To find the coefficient of discharge for the venture meter (Kvnt):

5. To find the coefficient of discharge for the orifice meter (Korf):


6. To find the coefficient of discharge for the Rotameter (Krota):

Results
Weight = 12 Kg
Table 2 – Results of calculated of finding the mass flow rate using different methods
| Run | ṁ Actual [kg/s] |
ṁ Rotameter [kg/s] |
ṁ Venturi [kg/s] |
ṁ Orifice [kg/s] |
|---|---|---|---|---|
| 1 | 0.46710782 | 0.43 | 0.451112186 | 0.40552304 |
| 2 | 0.44198895 | 0.39 | 0.408046325 | 0.61031692 |
| 3 | 0.37209302 | 0.35 | 0.363698271 | 0.54333742 |
| 4 | 0.32 | 0.31 | 0.326153571 | 0.52099885 |
| 5 | 0.28721876 | 0.27 | 0.277084521 | 0.4151797 |
| 6 | 0.24028835 | 0.24 | 0.241403461 | 0.36161668 |
| 7 | 0.2 | 0.19 | 0.204023162 | 0.30515846 |
| 8 | 0.15540016 | 0.15 | 0.160935641 | 0.24380191 |
Table 3 – Results of finding the coefficients of different methods
| Run | K Rotameter |
K Venturi |
K Orifice |
|---|---|---|---|
| 1 | 1.086297 | 1.035458 | 1.1518651 |
| 2 | 1.133305 | 1.083183 | 0.7241958 |
| 3 | 1.063123 | 1.023082 | 0.6848286 |
| 4 | 1.032258 | 0.981133 | 0.6142048 |
| 5 | 1.063773 | 1.036575 | 0.6917939 |
| 6 | 1.001201 | 0.995381 | 0.6644836 |
| 7 | 1.052632 | 0.980281 | 0.6553972 |
| 8 | 1.036001 | 0.965604 | 0.6374033 |
Average coefficients for the 8 runs of the different methods:
Average K of rotameter = 1.05857381
Average K of venturi-meter = 1.01258706
Average K of orifice = 0.72802154
Charts :
Comparing the actual mass flow rate with the one obtained by the different methods:
 |
| Fig 1 - The actual mass flow rate vs. the mass flow rate found from the Rotameter |
 |
| Fig 2 - The actual mass flow rate vs. the mass flow rate found from the Venturi |
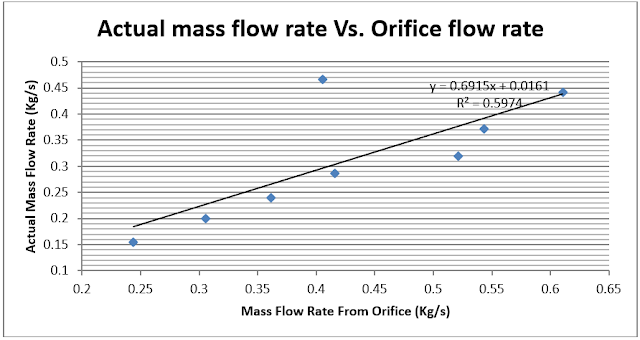 |
| Fig 3 - The actual mass flow rate vs. the mass flow rate found from the Orifice |
Discussion of results:
After doing the experiment calculations are done to calculate the mass flow rate form the Venturi-meter, Orifice and rotameter. Also, the actual mass flow rate is calculated then for the three parts we’ve calculated the coefficient of discharge. Finally the three charts above were plotted.In these three Figures the relation between the actual mass flow rate and each part is linear relation, so we can see that when the actual mass flow rate increases the mass flow rate obtained from each method increases.
It’s obvious that the orifice is the least accurate from the three parts, from the chart of the actual mass flow rate Vs. mass flow rate found from the Orifice which is Fig-3 point ( 0.4055 , 0.4671 ) has the biggest error. However, points in figures of “ actual mass flow rate Vs. the mass flow rate found from the rotameter” and “ actual mass flow rate Vs. mass flow rate found from the venture ” fits the line well, that means errors are not that large.
As for the discharge coefficients, the discharge coefficient for the venturi-meter was 1.01259 and the discharge coefficient of the rotameter is 1.058 which are almost 1; this indicates that the coefficient lies within the acceptable range of 0.9 to 1. However, the coefficient for the orifice does not lie within the acceptable range indicating the presence of errors. The orifice discharge coefficient is 0.7280 which is not possible as it indicates the gain of energy which is not true and this improves the results obtained in the Fig-3 as I said before.
As we know that every experiment may exists some kinds of errors, here in our experiment errors could exists from:
- Inaccuracy of measuring the time needs for balancing the arm carrying the water tank.
- The instability in the rotameter position.
- Truncation and formulas errors.
- Inaccuracy at reading hA, hB, hE and hF.
Conclusion:
This experiment aims to measure the mass flow rate of water using three methods: venutri-meter, orifice and rotameter. These mass flow rates are ideal and are compared with the actual rate measured using the water tank. However, these ideal mass flow rates are not consistent with the actual rate, and require an adjustment which is to be done using the discharge coefficients calculated for each method.Several conclusions can be deducted from the each method used. The coefficient of discharge for the venturi-meter and rotameter are close to our original assumption. However, this is not the case with the orifice, which indicates the presence of several errors which might include: incorrect reading of the water columns at points E and F.
It's noticed that the pressure difference reaches its highest value on the throat of the venturi meters’ tube due to the small cross sectional area.
Improving the results of the experiment can be achieved by not reading the values of the water height while looking perpendicularly, but our results are acceptable and we can say that they are precise somehow.







No comments: