The Center of Pressure - Fluid mechanics lab report
Abstract
The target of this experiment is to familiarize the student with the characteristics of the fluid on surface and how the distributed pressure forces which can be replaced by a resultant force exerted by the fluid affects the surface, and how the angle of the surface affects these effects.The line of action of the resultant force is acting on the normal direction into the plane; this point is called the pressure center at which the hydrostatic force acts. Then studying how the hydrostatic force varies with depth of the fluid then compare these quantities with the theoretical predictions.
In the experiment the data (balancing mass and fluid height) were taken for two angles 0˚ and 20˚ then the moment for both angles was calculated in both cases if submerged or fully merged, then graphs for moment vs. height and for moment vs. height cubed were plotted to calculate ૪1 and ૪2, then average ૪ was calculated and compared with the theoretical value.
Calculating the point of action of the pressure force on the plane surface for two values the assistant chosen, it acceptable. If the fluid contained behind a plane surface, it will cause a force effect on the surface which differ from fluid to another and depend on shape of surface. So this idea is very good in engineering in the design of bridges and it is used to know the factor of safety to avoid any failure in the bridges.
 |
| Pressure measurement |
Objectives
- To familiarize the students with basic effects of fluid on surfaces.
- How the angle affects the effect of the fluid on surfaces.
- Finding the point of action of the pressure force on the plane surface.
- Calculating the moment produced due fluid thrust in for two angles (0˚) and (20˚) in both cases if merged or submerged.
- Study how the hydrostatic force varies with depth of the fluid then compare these measurements with the theoretical analysis.
Results
Table No.2 - Results
for Angle θ = 0˚ with partially submerged (from 50 - 200 g the
surface is submerged in water)
| Partially submerged | Θ= 0ᵒ | ||||
|---|---|---|---|---|---|
| Weight (g) | h (mm) | R₁ cosΘ | Moment (N.m) | Mp (N.m) | Hᶟ (mᶟ) |
| 50 | 158 | 100 | 0.122575 | 2.446597 | 0.003944312 |
| 70 | 148 | 100 | 0.171605 | 2.348537 | 0.003241792 |
| 90 | 142 | 100 | 0.220635 | 2.309313 | 0.002863288 |
| 110 | 136 | 100 | 0.269665 | 2.270089 | 0.002515456 |
| 130 | 128 | 100 | 0.318695 | 2.201447 | 0.002097152 |
| 150 | 124 | 100 | 0.367725 | 2.191641 | 0.001906624 |
| 180 | 116 | 100 | 0.44127 | 2.147514 | 0.001560896 |
| 200 | 110 | 100 | 0.4903 | 2.10829 | 0.001331 |
Table No.3 - Results for Angle θ = 0˚ with fully submerged
(from 250 - 400 g the surface is fully merged in water)
| Fully submerged | Θ= 0ᵒ | ||
|---|---|---|---|
| Weight (g) | h (mm) | R₁ cosΘ | Moment (N.m) |
| 250 | 100 | 100 | 0.612875 |
| 270 | 94 | 100 | 0.661905 |
| 290 | 90 | 100 | 0.710935 |
| 310 | 86 | 100 | 0.759965 |
| 330 | 80 | 100 | 0.808995 |
| 350 | 76 | 100 | 0.858025 |
| 380 | 70 | 100 | 0.93157 |
| 400 | 66 | 100 | 0.9806 |
Table No.4 - Results for Angle θ = 20˚ with partially submerged (from 20 - 220 g the surface is submerged in water)
| Partially submerged | Θ=20ᵒ | ||||
|---|---|---|---|---|---|
| Weight (g) | h (mm) | R₁ cosΘ | Moment (N.m) | Mp (N.m) | Hᶟ (mᶟ) |
| 20 | 158 | 93.97 | 0.04903 | 2.373052 | 0.04903 |
| 40 | 148 | 93.97 | 0.09806 | 2.274992 | 0.09806 |
| 60 | 140 | 93.97 | 0.14709 | 2.20635 | 0.14709 |
| 90 | 128 | 93.97 | 0.220635 | 2.103387 | 0.220635 |
| 110 | 122 | 93.97 | 0.269665 | 2.064163 | 0.269665 |
| 160 | 108 | 93.97 | 0.39224 | 1.980812 | 0.39224 |
| 180 | 104 | 93.97 | 0.44127 | 1.971006 | 0.44127 |
| 200 | 100 | 93.97 | 0.4903 | 1.9612 | 0.4903 |
| 220 | 94 | 93.97 | 0.53933 | 1.921976 | 0.53933 |
Table No.5 - Results for Angle θ = 0˚ with fully
merged (from 240 - 400 g the surface is fully merged in water)
| Fully submerged | Θ=20ᵒ | ||
|---|---|---|---|
| Weight (g) | h (mm) | R₁ cosΘ | Moment (N.m) |
| 0.58836 | 93.97 | 90 | 240 |
| 0.63739 | 93.97 | 86 | 260 |
| 0.710935 | 93.97 | 80 | 290 |
| 0.759965 | 93.97 | 74 | 310 |
| 0.88254 | 93.97 | 64 | 360 |
| 0.93157 | 93.97 | 60 | 380 |
| 0.9806 | 93.97 | 56 | 400 |
Charts
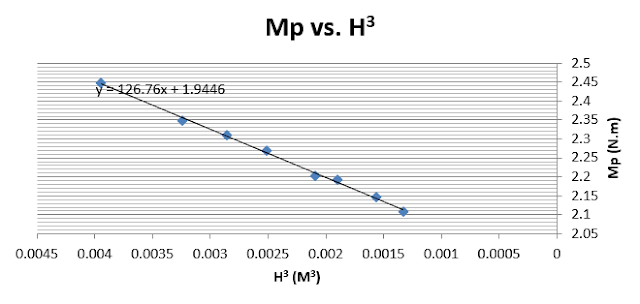 |
| Chart No.1: Mp vs. H3 for angle θ = 0˚ with partially submerged |
The relation between moment and h3 is linear as shown in the figure and the equation is:( y =126.76 x + 1.9446)
The relation between moment and h3 is linear as shown in the figure and the equation is:( y=137.18x+1.8188)
The relation between moment and h is reverse as shown in the figure and the equation is:( y = -0.0114 x +1.6)
Discussion of results:
After we collected our data from two different angels which are in table No.1, we made some calculations on them, these calculations gave us some results so we were able to calculate the moment for fully and partially submerged by taking this (h ≥ R1cos𝜃) or (h ≤ R1cos𝜃), each one of this has a special moment equation which are number 2 and 3 in the equations above.we used also equation 1 to find the moment and from this we can calculate the moment of partially submerged using equation 3. Using those equations leads us to but 4 tables which contain the resultant value, and there are table No.2 for partially submerged at , table No.3 for fully submerged at , table No.4 for partially submerged at , table No.5 for fully submerged at Some of those results in the four tables was plotted in 4 charts ( chart No.1, chart No.2, chart No.3,chart No.4 ) which all of them was a kind of linear functions.
we did the moment equation as a linear equation with h variable and compare it with the gradient of each chart we uses this to find the value of γ , in our sample calculations we uses the gradients of charts No.1 and No.2 and we found the average of them which gave us (9914 kg/m3) which is a near value of the theoretical value we uses (9806 kg/m3 ) these results could tell us that our experiment was good. The point of action was found by dividing the moment on the force which was calculated from the concept that says that the force equals the integral of pressure with the area change.
As human being we have to know that nothing is perfect and anything have to have errors, in our experiment errors may appear from the old tool we were using, also formula errors have a big effect in the values , digits also affect the accuracy of the results. It could also be from reading data as the high h ,or there are some leavings such as calcium and acetate or there are impurities in the water that was used so it can effect in reading data and made some error in experiment or in estimating when balance occurred when adding water. All of these and may be more may have an effect on our results but in general the experiment was made in a good way.
Conclusion:
One can conclude that the moment for the two angles 0ᵒ, 20ᵒ are increasing as the weight is increase, and the value of the moment between (0.04903-0.9806) N.m, and the height decrease as the mass increase. Take the height (angle zero), for weights between 50-400 gm, then we conclude from 50-200 gm the surface is submerged in the water. And from 250-400gm the surface is fully merged in water and from the graph moment Vs. h the relation is linear, and the height increasing as decreasing in moment (reverse relation).For angle 20, Take weights from 20-400gm and we conclude from 20-220gm the surface is submerged in water and the relation is linear and moment is increasing as h increasing.
And from 240-400gm the surface fully merged in water and the moment is decreasing when h is increasing so the relation is inverse. Pressure force on the plane surface depend on the type of fluid as when the density of fluid is high è increase pressure force, because of the relation between density and pressure force is proportional directly and the moment increase as the density . If the fluid contained behind a plane surface, it will cause a force effect on the surface which differ from fluid to another and depend on shape of surface. So this idea is very good in civil engineering in the design of bridge and they can know the factor of safety to avoid any failure in the bridges.
In this experiment, the moment due to the total fluid thrust on a fully and partially submerged plane surface were measured and then compared with the theoretical results. It is shown in the data that the calculated values are close to the theoretical ones. For water (the fluid used) γ = 9914 kg/m3. The values obtained in this experiment are relatively close to this value.
The main conclusion that has been reached after the experiment was carried out that if a fluid is to be contained behind a plane surface, this fluid exerts a force on that surface. This force depends on the fluid itself, its level and the shape and position of the surface. The results of the experiment were close to the expected theoretical results with some difference might be because of impurities in the water used. The plotted graphs were consistent with that expected from the equations used in the experiment with some little deviation could be ignored.









No comments: