PCM lab experiment | pulse code modulation

Introduction

There are many ways of impressing a communication signal on a carrier signal. There are also many types of communication channel, such as speech, music, television and data, and many carrier waveforms are possible. The most common form of waveform is the sinusoid, and sinusoidal carriers can differ from each other in amplitude, frequency of phase. Other waveforms are possible, of course, and indeed any waveform can theoretically be used as a carrier. However, only waveforms that have some advantage over the sinusoid are likely to find favor. A major attraction of the sinusoid is that it is easy to generate, but with the advent of integrated circuits, square waveforms have become increasingly popular.

This has allowed various communication administrations to economically implement square wave systems, which have theoretical attractions. These rely on exchanging bandwidth for noise, and fall into the general category of pulse code modulation (p.c.m.) systems. They make use of the fact that the transmitted signals are selected from a small choice of known types (e.g. square pulses of +V and –V only are allowable) to ensure that the receiver can nearly always correctly extract the signal from the noise of the transmission medium.

The Apparatus:

Figure 1 shows the apparatus, which comprises a pulse code modulator and demodulator. A choice of three or four bit encoding is available at the modulator. The pulse code demodulator supplied can reconstitute the signal. A difference amplifier is also supplied to allow the signal into the p.c.m. modulator to be compared with the signal out of the p.c.m. demodulator.

The following additional apparatus is required:

• Audio Signal Generator
• Oscilloscope

The Modulation Process

It is essential that in any modulation process the demodulated signal is the same as (or very nearly the same as) the signal applied to the modulator. The modulation process would be redundant of the signal was nor impaired in some way by the transmission medium connecting the source the signal to the reception point. The first task of the modulation process is therefore to impress the signal onto a carrier, which can contend more easily with the impairments of the chosen medium than the signal itself.

In the case of p.c.m. this carrier is a pulse stream. The pulses are grouped, and these groups are known as words. Every word gives some information about the signal, and if enough words are sent a complete description of, the waveform can be relayed. However, it is not necessary to send an infinite number of words because some information is already known: for example, the bandwidth of the signal being sent is often preset. Thus if the period of the highest frequency of the signal to be encoded is fm i.e. its period is 1/fm seconds, then the signal can be completely described by sending one word every 1/2fm seconds. This rate is known as the Nyquist rate, and implies that the waveform of the signal must be sampled at least 2fm times every second.

Usually it is the amplitude that is sampled, but it is possible to describe a waveform fully in terms of other parameters such as frequency and phase. Each word must now describe the amplitude of the signal at a particular point in time. As transmission systems do not normally employ storage, it is necessary to send one word between successive samples. This means that the original information signal, and the longer the word the greater the bandwidth. However, longer words give a better description of the amplitude so that a compromise is necessary between bandwidth and accurate reproduction of the signal at the demodulator. Pulses will be allowed only two states in the consideration that follows, but in practical transmission line systems information can be contained in three or four allowed states of signal.

The next section supplements the last two paragraphs with a description of the fundamental functions of the pulse code modulator and demodulator. Figure 2shows the block diagram of a simple three-bit word pulse code modulator, together with the significant waveforms.

The Modulator

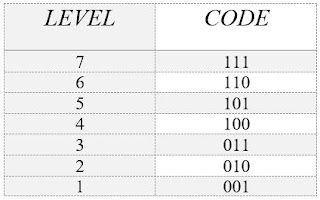
The signal to be transmitted is sampled at a rate usually a little greater than the Nyquist rate, i.e. at a frequency just above double the highest frequency of the information signal. In the example shown, the amplitude quantiser rounds off the sampled ‘spikes’ to the next allowable higher lever. In so doing information about the signal is irretrievable lost. The intervals between the allowable levels is not necessarily constant, and indeed ideally the levels are separated by intervals so that the probability of the samples falling into one level is the same as the probability of it falling into any other level. The determination of the best level separation is very difficult especially in the case of a single speech channel where different talkers differ in loudness yet the system must be designed to cater for all reasonable volumes.

The final part of the pulse code modulator is the coder, and this encodes each sample as a group (word) of binary digits. For reference, the Table gives the binary code for levels 1-7.

The Demodulator

Figure 3 shows the block diagram of the demodulator, together with the relevant waveforms. The binary signal received from the output of the transmission medium is decoded by taking groups of three binary digits and using the Table above, selecting the correct level to transmit from the encoder output. 

The encoder output is applied to a low pass filter, of bandwidth slightly less than half the sampling rate. In telephony systems the sampling rate is 8000 samples per second as this permits the use of relatively simple filters to provide the required bandwidth from 3000 Hz to 3400Hz; it also avoids interference from existing frequency division multiplex division multiplex equipment using carrier frequencies at 4kHz intervals.

In practical transmission, systems there is need to provide alignment information. This is to ensure that the receiver can fine the start of the word and is not trying to decode a combination the last part of one word and the first part of the following word. Alignment information usually takes the form of a unique word at intervals of many information words (a frame). For the purposes of this experiment the transmitter and receiver are interconnected to avoid the extra complexity of frame alignment words and a ‘word pulse’ terminal is supplied for triggering purposes.

Quantizing Distortion

When a three-bit word is being used only eight possible amplitudes can be transmitted to the encoder, out of the infinite number of possible amplitudes. The process of making the amplitudes of the samples correspond to discrete levels is termed quantizing and the amplitude errors introduced constitute quantizing noise. If the signal amplitude never exceeds the quantized range of amplitudes then the probability of the error signal exceeding any level between zero and S, the quantizing interval, falls linearly from 100 per cent to zero as the level in question varies from zero to S. This leads to the result that the mean square error noise is given by S2/12. If the signal exceeds the amplitude range, which is quantized, it is effectively clipped and the way in which quantizing and clipping noise depends upon the number of quantized levels and value of S is given in detail in Reference CSA.

Observations of Waveform

The first exercise is to observe the relationship between the binary words and the amplitude of the input. To facilitate this a d.c. supply is provided on the apparatus and by connecting this to the signal, input and observing the modulator output each of the possible binary words can be distinguished as the voltage is shifted from minimum to maximum. It is necessary to trigger from the word pulse terminal otherwise a bit train 100100 cannot be distinguished from 010010. For both 3 bit and 4 bit encoding all the possible codes should be identified. Notice that varying the bit rate does not affect the encoding process.


Applying a sinusoidal signal at a frequency of a few hundred Hz to the signal input, and adjusting the signal frequency for stable triggering, the modulator output can be seen to be cyclically reading through the code alphabet. By attaching, the modulator to the demodulator and observing the demodulator output the quantising effect of the pulse, code modulation process can be clearly seen. Varying the amplitude of the input signal so that it exceeds the extreme levels as determined by d.c enhances this observation. input test. With a reasonably high bit rate, and about 100Hz signal input, the number of levels allowable with each of 3 bit and 4 bit encoding can be easily counted. Increasing the amplitude beyond the maximum increases the length of time during which the sinusoid is clipped.


Applying a sinusoid to both the signal input and to terminal B of the difference amplifier, and connecting the demodulator output a terminal A, allows the quantisation noise to be examined. The observed shapes should be explained as the amplitude, bits per word, bit rate, and input signal frequency are varied. An r.m.s. meter should be used to measure the quantisation power and the effect of varying the frequency on this power should be measured and explained. A graph of quantisation power against input signal amplitude up to and beyond clipping should be drawn. Justify the shape of the curve beyond clipping. Is the value of quantisation noise power below clipping in agreement with the theoretical value derived in the previous section?

Suggestions for Further Experiments

The experimentation cab be readily further extended by inserting more complex waveforms (e.g. the 1kHz plus 3kHz supply on E15g or use an input from a microphone) at the signal input an observing and measuring the parameters of interest. A further impressive experiment is to listen to the demodulator output and observe the improvement in moving from 3 bit to 4 bit encoding, while attaining some subjective feel for the impairing effect on a pure sinusoid of quantisation noise and of various levels of clipping. In this latter experiment, the input signal should be used as a reference.

Procedure

1) First, we start by connect the Function Generator to the Oscilloscope immediately; to get a sinusoidal waveform with the frequency 3.4 kHz, and 1Vp-p amplitude.
2) Then, we connect the Function Generator to the p.c.m. Board at signal input. We should connect Dc supply to this input, too. In addition to that, we set the p.c.m. Board to on switch.
3) Fix the switch to 3 bit or 4 bit. In addition, set the bit rate switch to 40.
4) Connect the Oscilloscope to the Modulator Output, and receive the signal output, which is a square waveform. As it shows down.

5) After we get this result, we entered the output from the Modulator to the input of the Demodulator, and connect the output of the Demodulator directly to the Oscilloscope and get this waveform.

However, not in this clarity, it is just lines in parallel at horizontal manner, but close together and in linking them with a curve, you get the previous figure.

6) Finally, we connected the output from the Demodulator output to Op.Amp’s input, with a link from the Function Generator, and the Oscilloscope to the output of Op.Amp. So the result will be similar to the input waveform with some distortion, caused from the noise with the carrier wave.

Conclusion

• In this experiment, we observed the waveforms that result from the Modulator and the Demodulator. Modulator carry the input wave on a binary wave, and with some process it change the input wave, to a digital one using a Nyquist rate, and carry it to the output or sending machine.
• Demodulator process in reverse mode, so it changes the digital wave to it’s equivalent form, and then changing it to waveform – very near to sinusoidal wave- and it looks like the input wave, but not in 100 percent, because of the noise at the communications. Using specific filters could solve this problem.